LaTeXテンプレート大全-学術論文、レポート、サイト作成用使いやすいテンプレ一覧-

LaTex
2024.11.06

電子組版ソフトウェアのTeX、そのTeX上にマクロパッケージを組み込んで構築した文書処理システムがLaTeXです。基本的な機能のみを有しているTexとLaTeXを組み合わせて用いることで、組版をより手軽に行えます。

LaTeXを用いるときに役立つ公式のテンプレートを集めました。基本的なコードから記載しています。

次のリンクから知りたい情報へジャンプ！

文字・記号
ギリシャ文字
数学記号
数学テンプレート
演算子
数式テンプレート
括弧類

文字・記号

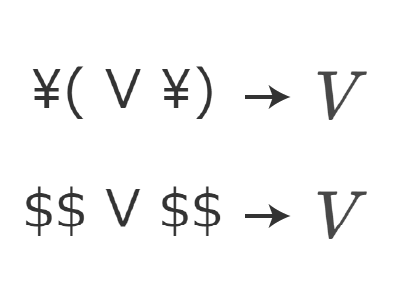
LaTeX一例

「\ ( コード \ ) 」もしくは「$2つずつでコードを挟む」ことで出力することができます。基本的な文字のコードから一覧にしました。

\と（でコードを囲むことで文章中に、$2つずつで囲むことで改行して中央揃えで記載されます。

ギリシャ文字

値を表す文字（定数,変数）

文字入力コード意味使用例
$$\pi$$\pi円周率
角度		 $$ V=\frac{4}{3}\pi r^3 $$
$$\mu$$\mu透磁率
摩擦係数
10-6		$$F= \mu N$$
$$\varepsilon$$\varepsilon誘電率
微小量		$$F=\frac{1}{4 \pi \varepsilon_0 }
\frac{Qq}{ r^2 }$$
$$\delta$$\delta微小変化$$ \delta = \frac{ P L^3 }{ 48 E I } $$
$$\Delta$$\Delta微小変化
行列式		$$\lim_{ \Delta x \rightarrow 0 }\Delta x = dx$$
$$\theta$$\theta角度$$\sin 2 \theta = 2 \sin \theta \cos \theta $$
$$\phi\; , \; \varphi$$\phi
\varphi		角度
ポテンシャル
波動関数		$$dv= r^2 \sin \theta dr d\theta d\varphi $$
$$\omega$$\omega角速度
1の３乗根		$$\omega = 2 \pi f \; , \;\omega ^3 =1 $$
$$\zeta$$\zeta1のn乗根$$ \zeta ^n =1 $$
$$\rho$$\rho密度
相関関数		$$ \rho \left( \boldsymbol{r} \right) $$
$$\sigma$$\sigma面密度
標準偏差		$$ \sigma \left( \boldsymbol{r} \right) $$
$$\gamma$$\gamma体積密度
比熱比		$$ \gamma \left( \boldsymbol{r} \right) $$
$$\lambda$$\lambda波長
固有値		$$ \lambda = \frac{ \upsilon }{ f } $$
$$\nu$$\nu振動数$$ \nu = \frac{ c }{ \lambda } $$
$$\upsilon$$\upsilon速度$$ E = h \nu = \frac{ 1 }{ v^2 } + W $$
$$\tau$$\tau時定数$$ f \left( t \right) = f \left( 0 \right) e ^ { -t/\tau } $$
$$\kappa$$\kappa曲率$$ \kappa = \frac{ 1 }{ r } $$

関数を表す文字

文字入力コード意味使用例
$$B$$Bベータ関数
$$\Gamma$$\Gammaガンマ関数
$$\Delta$$\Deltaデルタ関数
$$Z$$Zゼータ関数
$$\Phi \; , \; \varphi$$\Phi
\varphi		オイラーのファイ関数
特性関数
波動関数
$$\Psi \; , \; \varphi$$\Phi
\varphi		波動関数$$ \Psi = \sqrt{  \frac{2}{L}} \sin \frac{ n \pi }{L}x $$
$$X$$Xカイ二乗分布
$$\rho$$\rho相関関数
$$\Omega$$\Omega抵抗
$$M$$M平均
$$\sum$$\sum和$$\sum_{k=1}^{n}a_{k} = a_1 + a_2 + a_3 + \cdots + a_n $$
$$\prod$$\prod積$$\prod_{k=1}^{n}a_{k} = a_1 \times a_2 \times a_3 \times \cdots \times a_n $$

すべての文字

名称小文字大文字小文字コード大文字コード
アルファ$$\alpha$$$$A$$\alphaA
ベータ$$\beta$$$$B$$\betaB
ガンマ$$\gamma$$$$\Gamma$$\gamma\Gamma
デルタ$$\delta$$$$\Delta$$\delta\Delta
イプシロン$$\epsilon$$$$E$$\epsilonE
ゼータ$$\zeta$$$$Z$$\zetaZ
イータ$$\eta$$$$H$$\etaH
シータ$$\theta$$$$\Theta$$\theta\Theta
イオタ$$\iota$$$$I$$\iotaI
カッパ$$\kappa$$$$K$$\kappaK
ラムダ$$\lambda$$$$\Lambda$$\lambda\Lambda
ミュー$$\mu$$$$M$$\muM
ニュー$$\nu$$$$N$$\nuN
クシー$$\xi$$$$\Xi$$\xi\Xi
オミクロン$$o$$$$O$$oO
パイ$$\pi$$$$\Pi$$\pi\Pi
ロー$$\rho$$$$P$$\rhoP
シグマ$$\sigma$$$$\Sigma$$\sigma\Sigma
タウ$$\tau$$$$T$$\tauT
ユプシロン$$\upsilon$$$$\Upsilon$$\upsilon\Upsilon
ファイ$$\phi$$$$\Phi$$\phi\Phi
カイ$$\chi$$$$X$$\chiX
プシー$$\psi$$$$\Psi$$\psi\Psi
オメガ$$\omega$$$$\Omega$$\omega\Omega

数学記号

数式モードにおけて使用できる文字です。

よく使う記号

$$\pm$$\pm$$\mp$$\mp$$\times$$\times$$\div$$\div$$\leq$$\leq$$\theta$$\theta
$$\pi$$\pi$$\omega$$\omega$$\ell$$\ell$$\varepsilon$$\varepsilon$$\nabla$$\nabla$$\partial$$\partial

さまざまな記号

\( \pm \)

$$\sin$$\sin$$\cos$$\cos$$\tan$$\tan
$$\log$$\log$$\exp$$\exp$$\ln$$\ln
$$\pm$$\pm$$\mp$$\mp$$\times$$\times
$$\div$$\div$$\ast$$\ast$$\star$$\star
$$\circ$$\circ$$\bullet$$\bullet$$\cdot$$\cdot
$$\bigcirc$$\bigcirc$$\diamond$$\diamond$$\diamondsuit$$\diamondsuit
$$\clubsuit$$\clubsuit$$\heartsuit$$\heartsuit$$\spadesuit$$\spadesuit
$$\triangle$$\triangle$$\bigtriangleup$$\bigtriangleup$$\bigtriangledown$$\bigtriangledown
$$\triangleleft$$\traiangleleft$$\triangleright$$\triangleright$$\Re$$\Re
$$\Im$$\Im$$\surd$$\surd$$\top$$\top
$$\perp$$\perp$$\bot$$\bot$$\angle$$\angle
$$\imath$$\imath$$\jmath$$\jmath$$\hbar$$\hbar
$$\aleph$$\aleph$$\ell$$\ell$$\dagger$$\dagger
$$\ddagger$$\ddagger$$\leq$$\leq$$\geq$$\geq
$$\equiv$$\equiv$$\sim$$\sim$$\simeq$$\simeq
$$\approx$$\approx$$\neq$$\neq$$\propto$$\propto
$$\infty$$\infty$$\parallel$$\parallel$$\leftarrow$$\leftarrow
$$\Leftarrow$$\Leftarrow$$\rightarrow$$\rightarrow$$\Rightarrow$$\Rightarrow
$$\leftrightarrow$$\leftrightarrow$$\Leftrightarrow$$\Leftrightarrow$$\longleftarrow$$\longleftarrow
$$\Longleftarrow$$\Longleftarrow$$\longrightarrow$$\longrightarrow$$\Longrightarrow$$\Longrightarrow
$$\uparrow$$\uparrow$$\Uparrow$$\Uparrow$$\downarrow$$\downarrow
$$\Downarrow$$\Downarrow$$\updownarrow$$\updownarrow$$\Updownarrow$$\Updownarrow
$$\nearrow$$\nearrow$$\searrow$$\searrow$$\swarrow$$\swarrow
$$\nwarrow$$\nwarrow$$\backslash$$\backslash$$\flat$$\flat
$$\natural$$\natural$$\sharp$$\sharp$$\nabla$$\nabla
$$\partial$$\partial

次のリンクから知りたい情報へジャンプ！

文字・記号
ギリシャ文字
数学記号
数学テンプレート
演算子
数式テンプレート
括弧類

数学テンプレート

演算子

表示入力コード例
$$ + , – , \times , \div ,*$$\times
\div		+ , – , \times , \div ,*
$$x^2+y_i+z^3_j$$^ , _x^2+y_i+z^3_j
$$\frac{ \pi }{ 3 }$$\frac{ 分子 }{ 分母 }\frac{ \pi }{ 3 }
$$x < 0, y > 0$$ < , >x < 0, y > 0
$$x\text{≦}0, y\text{≧}0$$\text{≦}
\text{≧}		x \text{≦} 0, y \text{≧} 0
$$x\leq0,y\geq0$$\leq
\geq		x \leq 0,y \geq 0
$$x\ll0, y\gg0$$\ll, \ggx \ll 0, y \gg 0
$$x\neq1$$\neqx \neq 1
$$x\unicode{x2252}0$$\unicode{x2252}x \unicode{x2252} 0
$$z \simeq 1$$\simeqz \simeq 1
$$x_1\cdot x_2 \cdots x_n \\
\cdots x_i \dots x_j \ldots $$		\cdot
\cdots
\dots
\ldots		x_1 \cdot x_2 \cdots x_n

\cdots x_i \dots x_j \ldots
表示入力コード例
$$AB/\!/XY$$/\!/AB/\!/XY
$$\triangle ABC\\\equiv\\\triangle DEF$$\equiv\triangle ABC\equiv\triangle DEF
$$
z \unicode
{x2254} 3
\\

w \unicode
{x2255} 4
$$		\unicode
{x2254}
\unicode
{x2255}		z \unicode
{x2254} 3
w \unicode
{x2255} 4
$$1\subset X \\
X\supset x$$		\subset
\supset		1\subset X
X\supset x
$$1\in Y \\
Y \ni y$$		\in
\ni		1 \in Y
Y \ni y
$${}_n C_k$${}_
{文字}
_		{}_n C_k
$$\log{2}x$$\log{底}数式\log{2}x
$$\log y$$\log 数式\log y
$$\exp(z)$$\exp(数式)\exp(z)
$$\hat{\boldsymbol{x}}$$\hat{文字}\hat{\boldsymbol{x}}
$$\left\langle{x}\middle|{y}\right\rangle$$\left\langle{文字}
\middle|
{文字}\right\rangle		\left\langle{x}\middle|{y}\right\rangle

数式テンプレート

簡単な数式

名称表示テンプレート備考(使用プログラム)
分数$$\frac{1}{4\pi\varepsilon_{0}}$$\frac{1}{4\pi\varepsilon_{0}}
微分$$\frac{dy}{dx}+ \frac{ \partial f }{ \partial x }+\frac{ \partial F_x\left( \boldsymbol{r} \right) }{ \partial x }$$\frac{dy}{dx} +
\frac{ \partial f }{ \partial x } +
\frac{ \partial F_x\left( \boldsymbol{r} \right) }
{ \partial x }
積分$$\int_{0}^{2\pi}\frac{1}{2}x dx$$\int_{0}^{2\pi}\frac{1}{2}x dx
極限$$\lim_{h \to 0} \frac{\sqrt{a+h}-\sqrt{a}}{h}$$\lim_{h \to 0} \frac{\sqrt{a+h}-\sqrt{a}}{h}
合計$$\sum_{i=1}^{n}a_{i}$$\sum_{i=1}^{n}a_{i}
行列$$A = \left(
\begin{array}{ccc}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}
\right)$$		A = \left(
￥begin{array}{ccc}
1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}
\right)

全角￥を半角\に置き換え		begin{array}{cc}：中央揃え
begin{array}{rr}：右揃え
begin{array}{ll}：左揃え

複雑な数式

名称表示テンプレート備考(使用プログラム)
周回積分$$\displaystyle \oint_0^1 f(x) dx$$\displaystyle \oint_0^1 f(x) dx\displaystyleか”$$”を前後で囲い
ディスプレイモードに
直角座標系$$ \boldsymbol{A}\left( \boldsymbol{r} \right)= A_x\left( \boldsymbol{r} \right)\hat{\boldsymbol{x}}+A_y\left( \boldsymbol{r} \right)\hat{\boldsymbol{y}}+A_z\left( \boldsymbol{r} \right)\hat{\boldsymbol{z}}$$\boldsymbol{A}\left( \boldsymbol{r} \right)= A_x\left( \boldsymbol{r} \right)\hat{\boldsymbol{x}}+A_y\left( \boldsymbol{r} \right)\hat{\boldsymbol{y}}+A_z\left( \boldsymbol{r} \right)\hat{\boldsymbol{z}}\eqalign{ 数式 }で囲う
円柱座標系$$\boldsymbol{B}\left( \boldsymbol{r} \right)= B_\rho\left( \boldsymbol{r} \right)\hat{\boldsymbol{\rho}}+B_z\left( \boldsymbol{r} \right)\hat{\boldsymbol{z}}$$\boldsymbol{B}\left( \boldsymbol{r} \right)= B_\rho\left( \boldsymbol{r} \right)\hat{\boldsymbol{\rho}}+A_z\left( \boldsymbol{r} \right)\hat{\boldsymbol{z}}￥begin{align} 数式 \end{align}
で囲う
球座標系$$\boldsymbol{C}\left( \boldsymbol{r} \right)= C_r\left( \boldsymbol{r} \right)\hat{\boldsymbol{r}}$$\boldsymbol{C}\left( \boldsymbol{r} \right)= C_r\left( \boldsymbol{r} \right)\hat{\boldsymbol{r}}\langleが”〈”を表す
微小体積$$
dv=\begin{cases}
dxdydz \\
\rho d\rho d\phi dz \\
r^2sin\theta dr d\theta d\phi \end{cases}
$$		dv=￥begin{cases}
dxdydz \\
\rho d\rho d\phi dz \\
r^2sin\theta dr d\theta d\phi \end{cases}

全角￥を半角\に置き換え		\cases{ ~ }
でも可
￥begin{array} ~
\end{array}
でも可
括弧の大きさに差
勾配
gradiant		$$ \nabla f\left( \boldsymbol{r} \right)=
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial x }\hat{\boldsymbol{x}}+
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial y }\hat{\boldsymbol{y}}+
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial z }\hat{\boldsymbol{z}}
$$		\nabla f\left( \boldsymbol{r} \right)
=
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial x }\hat{\boldsymbol{x}}
+
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial y }\hat{\boldsymbol{y}}
+
\frac{ \partial f\left( \boldsymbol{r} \right) }{ \partial z }\hat{\boldsymbol{z}}		|の前に\が付く
発散
divergence		$$ \nabla \boldsymbol{F}\left( \boldsymbol{r} \right)=
\frac{ \partial F_x\left( \boldsymbol{r} \right) }{ \partial x }+
\frac{ \partial F_y\left( \boldsymbol{r} \right) }{ \partial y }+
\frac{ \partial F_z\left( \boldsymbol{r} \right) }{ \partial z }
$$		\nabla \boldsymbol{F}\left( \boldsymbol{r} \right)
=
\frac{ \partial F_x\left( \boldsymbol{r} \right) }{ \partial x }
+
\frac{ \partial F_y\left( \boldsymbol{r} \right) }{ \partial y }
+
\frac{ \partial F_z\left( \boldsymbol{r} \right) }{ \partial z }
回転
rotation		$$ \eqalign{& \nabla \times \boldsymbol{F}\left( \boldsymbol{r} \right) \\ &=
\left( \frac{ \partial F_z }{ \partial y } –
\frac{ \partial F_y }{ \partial z } \right)\hat{\boldsymbol{x}}+
\left( \frac{ \partial F_x }{ \partial z } –
\frac{ \partial F_z }{ \partial x } \right)\hat{\boldsymbol{y}}+
\left( \frac{ \partial F_y }{ \partial x } –
\frac{ \partial F_x }{ \partial y } \right)\hat{\boldsymbol{z}}
\\ &=
\left|
\begin{array}{ccc}
\hat{\boldsymbol{x}} & \hat{\boldsymbol{y}} & \hat{\boldsymbol{z}} \\
\frac{ \partial }{ \partial x } & \frac{ \partial }{ \partial y } & \frac{ \partial }{ \partial z } \\
F_x & F_y & F_z
\end{array}
\right|
}$$		\eqalign{& \nabla \times \boldsymbol{F}\left( \boldsymbol{r} \right) \\
&=
\left( \frac{ \partial F_z }{ \partial y } –
\frac{ \partial F_y }{ \partial z } \right)\hat{\boldsymbol{x}}+
\left( \frac{ \partial F_x }{ \partial z } –
\frac{ \partial F_z }{ \partial x } \right)\hat{\boldsymbol{y}}+
\left( \frac{ \partial F_y }{ \partial x } –
\frac{ \partial F_x }{ \partial y } \right)\hat{\boldsymbol{z}}\\
&=
\left|
￥begin{array}{ccc}
\hat{\boldsymbol{x}} & \hat{\boldsymbol{y}} & \hat{\boldsymbol{z}} \\
\frac{ \partial }{ \partial x } & \frac{ \partial }{ \partial y } & \frac{ \partial }{ \partial z } \\
F_x & F_y & F_z
\end{array}
\right|
}
全角￥を半角\に置き換え
ガウスの
定理		$$
\oint_S \boldsymbol{F}
\left( \boldsymbol{r} \right) \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) \;dS
=
\int_v \nabla \cdot \boldsymbol{F}
\left( \boldsymbol{r} \right) \;dv
$$		\oint_S \boldsymbol{F}
\left( \boldsymbol{r} \right) \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) dS
=
\int_v \nabla \cdot \boldsymbol{F}
\left( \boldsymbol{r} \right) dv
ストークスの定理$$
\oint_C \boldsymbol{F}
\left( \boldsymbol{r} \right) d\boldsymbol{\ell}
=
\oint_v \left\{\nabla \times \boldsymbol{F}
\left( \boldsymbol{r} \right) \right\} \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) \;dS
$$		\oint_C \boldsymbol{F}
\left( \boldsymbol{r} \right) d\boldsymbol{\ell}
=
\oint_v \left\{\nabla \times \boldsymbol{F}
\left( \boldsymbol{r} \right) \right\} \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) dS
クーロンの
法則		$$
\eqalign{
\boldsymbol{F}
\left( \boldsymbol{r_0} \right)
&=
\frac{1}{ 4 \pi \varepsilon_0 }
\frac{ Q_0Q_1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| ^2 }
\hat{\boldsymbol{R}}
\\ &=
\frac{Q_0Q_1}{ 4 \pi \varepsilon_0 }
\frac{ \boldsymbol{r}_0 – \boldsymbol{r}_1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| ^3 }
}$$		\eqalign{
\boldsymbol{F}
\left( \boldsymbol{r_0} \right)
&=
\frac{1}{ 4 \pi \varepsilon_0 }
\frac{ Q_0Q_1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| ^2 }
\\ &=
\frac{Q_0Q_1}{ 4 \pi \varepsilon_0 }
\frac{ \boldsymbol{r}_0 – \boldsymbol{r}_1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| ^3 }
}		$$
\hat{\boldsymbol{R}} =
\frac{ \boldsymbol{r}_0 – \boldsymbol{r}_1 }{ \left|
\boldsymbol{r}_0 – \boldsymbol{r}_1 \right| }
$$であることを利用
電界$$
\eqalign{
\boldsymbol{E}
\left( \boldsymbol{r} \right)
&=
\frac{Q_1}{ 4 \pi \varepsilon_0 }
\frac{ \boldsymbol{r} – \boldsymbol{r}_1 }{ \left| \boldsymbol{r} – \boldsymbol{r}_1 \right| ^3 }
}$$		\eqalign{
\boldsymbol{E}
\left( \boldsymbol{r} \right)
&=
\frac{Q_1}{ 4 \pi \varepsilon_0 }
\frac{ \boldsymbol{r} – \boldsymbol{r}_1 }
{ \left| \boldsymbol{r} – \boldsymbol{r}_1 \right| ^3 }
}
電位$$
\eqalign{ V
\left( \boldsymbol{r} \right)
&=
\frac{Q_1}{ 4 \pi \varepsilon_0 }
\frac{ 1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| }
}$$		\eqalign{ V
\left( \boldsymbol{r} \right)
&=
\frac{Q_1}{ 4 \pi \varepsilon_0 }
\frac{ 1 }{ \left| \boldsymbol{r}_0 – \boldsymbol{r}_1 \right| }
}
電界→電位$$
\boldsymbol{E}
\left( \boldsymbol{r} \right)
= \; – \nabla \cdot V
\left( \boldsymbol{r} \right)
$$		\boldsymbol{E}
\left( \boldsymbol{r} \right)
= \; – \nabla \cdot V
\left( \boldsymbol{r} \right)
ガウスの
法則
（積分形）		$$
\int_S \boldsymbol{E}
\left( \boldsymbol{r} \right) \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) \;dS
=
\frac{1}{ \varepsilon_0 }
\int_v \rho \left( \boldsymbol{r} \right) dv
$$		\int_S \boldsymbol{E}
\left( \boldsymbol{r} \right) \cdot
\hat{\boldsymbol{n}}
\left( \boldsymbol{r} \right) \;dS
=
\frac{1}{ \varepsilon_0 }
\int_v \rho \left( \boldsymbol{r} \right) dv
ガウスの
法則
（微分形）		$$
\nabla \cdot \boldsymbol{E}
\left( \boldsymbol{r} \right) \cdot
=
\frac{\rho \left( \boldsymbol{r} \right)}{ \varepsilon_0 }
$$		\nabla \cdot \boldsymbol{E}
\left( \boldsymbol{r} \right) \cdot
=
\frac{\rho \left( \boldsymbol{r} \right)}{ \varepsilon_0 }

次のリンクから知りたい情報へジャンプ！

文字・記号
ギリシャ文字
数学記号
数学テンプレート
演算子
数式テンプレート
括弧類

括弧類

左右装飾

括弧の種類
名称表示テンプレート備考(使用プログラム)
丸括弧$$\left( \frac{1}{6} \right)$$\left( \frac{1}{6} \right)
波括弧$$\left\{ \frac{1}{6} \right\}$$\left\{ \frac{1}{6} \right\}{}の前に¥が付く
四角括弧$$\left[ \frac{1}{6} \right]$$\left[ \frac{1}{6} \right]
三角括弧$$\left\langle \frac{1}{6} \right\rangle$$\left\langle \frac{1}{6} \right\rangle\langleが”〈”を表す
絶対値$$\left| \frac{1}{6} \right|$$\left| \frac{1}{6} \right|
ノルム
（ベクトルの大きさ）		$$\left\| \frac{1}{6} \right\|$$\left\| \frac{1}{6} \right\||の前に\が付く
組み合わせ$$\left(\left| \frac{1}{6} \right|\right)$$\left(\left| \frac{1}{6} \right|\right)
サイズ変更
名称表示テンプレート備考(使用プログラム)
標準$$\ ( \frac{a}{b} ) $$\( \frac{a}{b} )
小$$\bigl( \frac{a}{b} \bigr)$$\bigl( \frac {a}{b} \bigr)
中$$\Bigl( \frac{a}{b} \Bigr)$$\Bigl( \frac{a}{b} \Bigr)
大$$\biggl( \frac{a}{b} \biggr)$$\biggl( \frac{a}{b} \biggr)
極大$$\Biggl( \frac{a}{b} \Biggr)$$\Biggl( \frac{a}{b} \Biggr)
自動$$\left( \frac{a}{b} \right)$$\left( \frac{a}{b} \right)
場所指定$$,\Bigl( \frac{a}{b} \Bigr),\Bigm( \frac{a}{b} \Bigm),\Bigr( \frac{a}{b} \Bigl),$$,\Bigl( \frac{a}{b} \Bigr)
,\Bigm( \frac{a}{b} \Bigm)
,\Bigr( \frac{a}{b} \Bigl),		場所指定なし\Big
場所指定左\Bigl
場所指定中央\Bigm
場所指定右\Bigr

場所指定”m”は区切り文字に使うと良い
片側$$f(x) =\begin{cases}\infty & (x = 0) \\ x^2 & (x \neq 0) \end{cases}$$f(x) =
￥begin{cases}\infty & (x = 0) \\ 
x^2 & (x \neq 0) \end{cases}

全角￥を半角\に置き換え

上下装飾

名称表示テンプレート備考(使用プログラム)
ルート（根号）$$\sqrt {a_1 + a_2}\\\\\sqrt[ 3 ]{ a_1^2 + a_1^2 }$$\sqrt {a_1 + a_2}

\sqrt[ 3 ]{ a_1^2 + a_1^2 }
上部括弧$$\overbrace{ a_1 + \cdots + a_n }^{ n }$$\overbrace{ a_1 + \cdots + a_n }^{ n }
下部括弧$$\overbrace{ a_1 + \cdots + a_n }_{ n }$$\overbrace{ a_1 + \cdots + a_n }_{ n }
下部括弧
(+上部装飾)		$$\underbrace{ a_1 + \cdots + a_n }_{ n }^{(note \;note)}$$\underbrace{ a_1 + \cdots + a_n }_{ n }^{(note \;note)}
上部装飾$$\overrightarrow{AB}$$\overrightarrow{AB}\overline
\overrightarrow
\overleftarrow
\overleftrightarrow
\overRightarrow
\overLeftarrow
\overLeftrightarrow
など
下部装飾$$\underline{x_1^2-x_2+3}$$\underline{x_1^2-x_2+3}\underline
\underrightarrow
\underleftarrow
\underleftrightarrow
\underRightarrow
\underLeftarrow
\underLeftrightarrow
など

次のリンクから知りたい情報へジャンプ！

文字・記号
ギリシャ文字
数学記号
数学テンプレート
演算子
数式テンプレート
括弧類

その他

テクニック

名称表示テンプレート備考(使用プログラム)
周回積分$$\displaystyle \oint_0^1 f(x) dx$$\displaystyle \oint_0^1 f(x) dx\displaystyleか”$$”を前後で囲い
ディスプレイモードに
式を揃える$$ \eqalign{\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt}$$\displaystyle \eqalign{\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt}\eqalign{ 数式 }で囲う
式を揃える$$\begin{align}\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}$$￥begin{align}\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}
￥を半角にする		￥begin{align} 数式 \end{align}
で囲う
三角括弧$$\left\langle \frac{1}{6} \right\rangle$$\left\langle \frac{1}{6} \right\rangle\langleが”〈”を表す
絶対値$$\left| \frac{1}{6} \right|$$\left| \frac{1}{6} \right|
ノルム
（ベクトルの大きさ）		$$\left\| \frac{1}{6} \right\|$$\left\| \frac{1}{6} \right\||の前に\が付く
組み合わせ$$\left(\left| \frac{1}{6} \right|\right)$$\left(\left| \frac{1}{6} \right|\right)

視覚表現

名称表示テンプレート備考(使用プログラム)
表$$
\begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\ \hline f’ \left(x \right) & + & 0 & – & 0 & + \\ \hline f \left(x \right) & \nearrow & e & \searrow & -e & \nearrow \end{array}
$$		￥begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline f’ x & + & 0 & – & 0 & + \\
\hline f x & \nearrow & e & \searrow & -e & \nearrow \end{array}
全角￥を半角\に置き換え		改行は”\\”
大きな
行列		$$ \begin{eqnarray}\left(\begin{array}{cccc}x_{ 11 } & x_{ 12 } & \ldots & x_{ 1n } \\x_{ 21 } & x_{ 22 } & \ldots & x_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ x_{ m1 } & x_{ m2 } & \ldots & X_{ mn }\end{array}\right)\end{eqnarray}
$$		￥begin{eqnarray}\left(￥begin{array}{cccc}x_{ 11 } & x_{ 12 } & \ldots & x_{ 1n } \\x_{ 21 } & x_{ 22 } & \ldots & x_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ x_{ m1 } & x_{ m2 } & \ldots & X_{ mn }\end{array}\right)\end{eqnarray}
全角￥を半角\に置き換え		“\vdots”
縦３ドット
“\ddots”
横３ドット
“\ldots”
右斜下３ドット
式を揃える$$\begin{align}\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}$$￥begin{align}\int fx \,dx &= \int f(g(t)) \frac{dx}{dt} \,dt \\ &= \int f(g(t))g’(t) \,dt \end{align}
￥を半角にする		￥begin{align} 数式 \end{align}
で囲う
三角括弧$$\left\langle \frac{1}{6} \right\rangle$$\left\langle \frac{1}{6} \right\rangle\langleが”〈”を表す
絶対値$$\left| \frac{1}{6} \right|$$\left| \frac{1}{6} \right|
ノルム
（ベクトルの大きさ）		$$\left\| \frac{1}{6} \right\|$$\left\| \frac{1}{6} \right\||の前に\が付く
組み合わせ$$\left(\left| \frac{1}{6} \right|\right)$$\left(\left| \frac{1}{6} \right|\right)

$$
\begin{array}{c|ccccc} x & \cdots & -1 & \cdots & 1 & \cdots \\ \hline f’ x & + & 0 & – & 0 & + \\ \hline f x & \nearrow & e & \searrow & -e & \nearrow \end{array}
$$

次のリンクから知りたい情報へジャンプ！

文字・記号
ギリシャ文字
数学記号
数学テンプレート
演算子
数式テンプレート
括弧類

参考文献

LaTexの特殊文字・特別記号 大東文化大学

スポンサーリンク

Solverwp- WordPress Theme and Plugin

タイトルとURLをコピーしました